Giải chi tiết Đề thi vào lớp 10 chuyên Lý - Dạy học sáng tạo - 120424

Xin giới thiệu đến các bạn lời Giải chi tiết Đề thi vào lớp 10 chuyên Lý - Dạy học sáng tạo - 120424 của trung tâm DẠY HỌC SÁNG TẠO phát hành ngày 12 tháng 4 năm 2024, nhằm giúp các em học sinh rèn luyện thêm kĩ năng chuẩn bị bước vào kì thi tuyển sinh lớp 10 chuyên Vật lý.

Nếu chưa có Đề thi vào lớp 10 chuyên Lý - Dạy học sáng tạo - 120424, các em có thể xem tại đây: Đề thi vào lớp 10 chuyên Lý - Dạy học sáng tạo - 120424

Câu I

1. Khoảng cách giữa hai thuyền sau thời gian 10 phút kế từ khi chúng xuất phát

Vận tốc thuyền đi xuôi dòng $$\begin{align} v_\text{x}&=v+u\\ &=5+2=7\ \text{m/s} \end{align}$$ Vận tốc thuyền đi ngược dòng $$\begin{align} v_\text{n}&=v-u\\ &=5-2=3\ \text{m/s} \end{align}$$ Do hai thuyền chạy ngược chiều nhau nên khoảng cách giữa hai thuyền sau thời gian $t_0=10\ \text{min}=600\ \text{s}$ được tính bằng $$\begin{align} d_1&=\left(v_\text{x}+v_\text{n}\right)\cdot t_1\\ &=\left(7+3\right)\cdot 600=6000\ \text{m} \end{align}$$ 2. Hai thuyền quay lại và về điểm xuất phát cùng lúc
a. Tỉ số $\frac{t_1}{t_2}$ Quãng đường thuyền đi xuôi với thời gian $t_1$ là $$s_\text{x}=v_\text{x}t_1$$ Quãng đường thuyền đi ngược với thời gian $t_2$ là $$s_\text{n}=v_\text{n}t_2$$ Vẫn các quãng đường đó, các vật đi quay lại nơi xuất phát sẽ mất các thời gian $$t_1'=\frac{s_\text{x}}{v_\text{n}}=\frac{v_\text{x}}{v_\text{n}}t_1\\ t_2'=\frac{s_\text{n}}{v_\text{x}}=\frac{v_\text{n}}{v_\text{x}}t_2$$ Tổng thời gian cả đi và về của các thuyền bằng nhau và bằng $$\begin{align} t=t_1+t_1'=t_2+t_2'\\ \end{align}$$ Tức là $$t_1+\frac{v_\text{x}}{v_\text{n}}t_1=t_2+\frac{v_\text{n}}{v_\text{x}}t_2$$ Suy ra tỉ số $$\begin{align} \frac{t_1}{t_2}&=\frac{1+\frac{v_\text{n}}{v_\text{x}}}{1+\frac{v_\text{x}}{v_\text{n}}}\\ &=\frac{1+\frac{3}{7}}{1+\frac{7}{3}}\\ &=\frac{3}{7} \end{align}$$ b. Khoảng cách lớn nhất giữa hai thuyền
Ta có thể vẽ đồ thị biểu diễn chuyển động của các thuyền.
Trên đồ thị ta thấy khoảng cách xa nhất giữa hai thuyền bằng khoảng cách giữa chúng khi thuyền đi xuôi bắt đầu đổi chiều chuyển động, khoảng cách này là $$\begin{align} d_\text{max}&=t_1\left(v_\text{x}+v_\text{n}\right)\\ \end{align}$$ Trong đó $t_1$ được xác định từ hệ phương trình $$\begin{cases} \frac{t_1}{t_2}=\frac{3}{7}\\ t_1+t_2=30\cdot 60 \end{cases}$$ $$\Rightarrow t_1=540\ \text{s}$$ Bây giờ $$\begin{align} d_\text{max}&=t_1\left(v_\text{x}+v_\text{n}\right)\\ &=540\left(7+3\right)\\ &=5400\ \text{m} \end{align}$$

Câu II

1. Nhiệt lượng từ chiếc thìa truyền sang cốc nước lạnh
Nhiệt độ ban đầu của thìa là $𝑡_1$. Sau khi nhúng vào cốc nước lạnh có nhiệt độ $𝑡_2$, chiếc thìa truyền nhiệt lượng $$Q_\text{t}=m_\text{t}c_\text{t}\left(t_1-t_\text{n1}\right)$$ Trong đó $t_\text{n1}$ là nhiệt độ cân bằng của thìa và nước. Phương trình cân bằng nhiệt là $$m_\text{t}c_\text{t}\left(t_1-t_\text{n1}\right)=DV_2c\left(t_\text{n1}-t_2\right)\\ $$ $$t_{\mathrm{n} 1}=\frac{m_{\mathrm{t}} c_{\mathrm{t}} t_1+\rho V_2 c t_2}{m_{\mathrm{t}} c_{\mathrm{t}}+\rho V_2 c} \approx 10.70\ ^{\circ}\mathrm{C}$$ Bây giờ thì ta tính được nhiệt lượng $$Q_{\mathrm{t}}=\frac{m_{\mathrm{t}} c_{\mathrm{t}} \rho V_2 c}{m_{\mathrm{t}} c_{\mathrm{t}}+\rho V_2 c}\left(t_1-t_2\right) \approx 1.468 \mathrm{~kJ} .$$ 2. Độ giảm nhiệt độ của tách trà sau khi bỏ chiếc thìa trở lại
Sau khi nhúng lại thìa vào tách trà, quá trình trao đổi nhiệt sẽ lại xảy ra và nhiệt độ cân bằng của trà là $𝑡_\text{t2}$. Phương trình cân bằng nhiệt $$m_\text{t}c_\text{t}\left(t_\text{t2}-t_\text{n1}\right)=DV_1c\left(t_\text{n1}-t_\text{t2}\right)$$ $$t_{\mathrm{t} 2}=\frac{m_{\mathrm{t}} c_{\mathrm{t}} t_{\mathrm{n} 1}+\rho V_1 c t_1}{m_{\mathrm{t}} c_{\mathrm{t}}+\rho V_1 c} \approx 78.3\ ^{\circ} \mathrm{C} \text {. }$$ Nhiệt độ của tách trà đã giảm đi $$\Delta t_1=-1.7\ ^\text{o}\text{C}$$ 3. Nhiệt độ thấp nhất có thể đạt được nếu cứ đưa chiếc thìa qua lại giữa tách trà và cốc nước
Nhiệt độ thấp nhất đạt được khi nhiệt độ trà không giảm được nữa và nhiệt độ nước lạnh không tăng được nữa. Điều này chỉ xảy ra khi nhiệt độ của cả trà, thìa và nước lạnh bằng nhau. Nhiệt độ đó ta đặt là $t_\text{min}$. Áp dụng phương trình cân bằng nhiệt $$\left(m_{\mathrm{t}} c_{\mathrm{t}}+\rho V_1 c\right)\left(t_1-t_{\mathrm{min}}\right)=\rho V_2 c\left(t_{\mathrm{min}}-\mathrm{t}_2\right),$$ $$t_{\mathrm{min}}=\frac{\left(m_{\mathrm{t}} c_{\mathrm{t}}+\rho V_1 c\right) t_1+\rho V_2 c t_2}{m_{\mathrm{t}} c_{\mathrm{t}}+\rho\left(V_1+V_2\right) c}=30.4\ ^{\circ} \mathrm{C}$$ 4. Số lần chuyển để nhiệt độ đạt thấp nhất
Ông Năm có thể kết luận rằng sự chênh lệch nhiệt độ thu được là $80\ \text{°C} − 30.4\ \text{°C} = 49.6\ \text{°C}$ là xấp xỉ 29 lần mức giảm của $1.7\ \text{°C}$ ($49.6 / 1.7 \approx 29$). Như lời giải ở phần 1. cho thấy, nhiệt lượng truyền phụ thuộc vào chênh lệch nhiệt độ giữa trà và nước. Tuy nhiên, sự chênh lệch này giảm dần sau mỗi lần chuyển, do đó, nhiệt độ sẽ không ở mức $1.7\ \text{°C}$ mỗi lần. Số lần truyền nhiệt bằng thìa sẽ phải rất lớn, về mặt lý thuyết là vô hạn. Vậy là dự đoán của ông Năm đã sai.

Câu III

1. Các số chỉ ampe kế $\text{A}_1$, số chỉ vôn kế $\text{V}_1$ và hiệu điện thế $U$
Ta quy ước các điện trở và các điểm nút như hình dưới đây:

Hình 2: Mạch điện đã được quy ước thêm các điểm nút: A, B, M, N, P, Q, G và các điện trở được đánh số thứ tự 1, 2, 3, 4, 5.

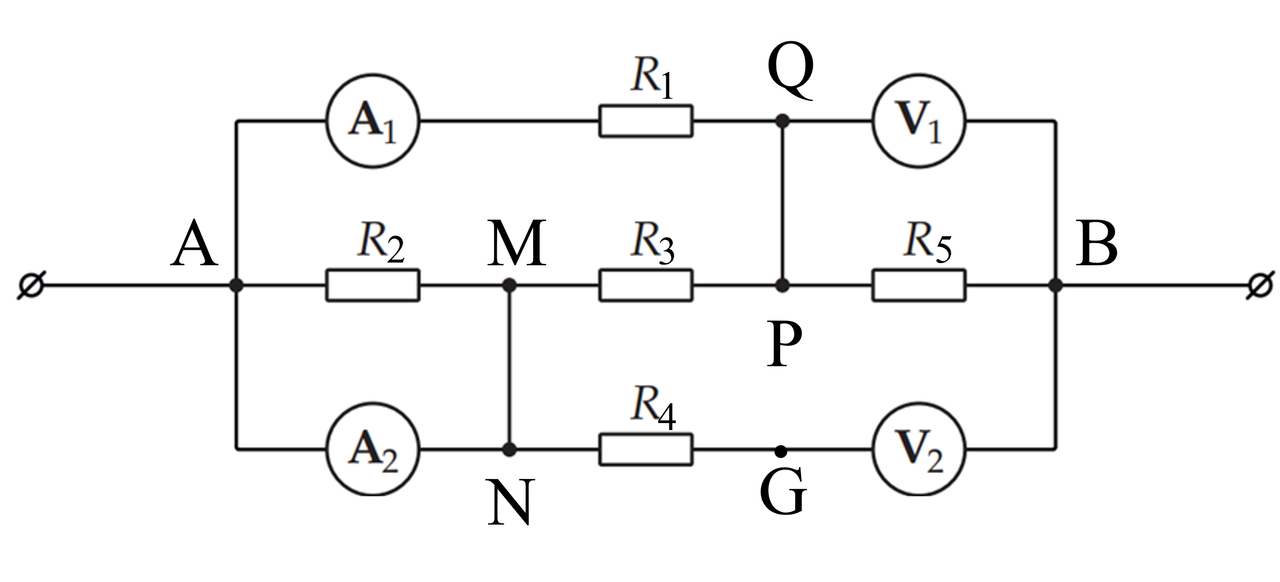
Ta vẽ lại mạch như hình dưới đây theo quy tắc chập các nút và bỏ các nhánh có vôn kế:

Hình 3: Mạch điện đã được vẽ lại.

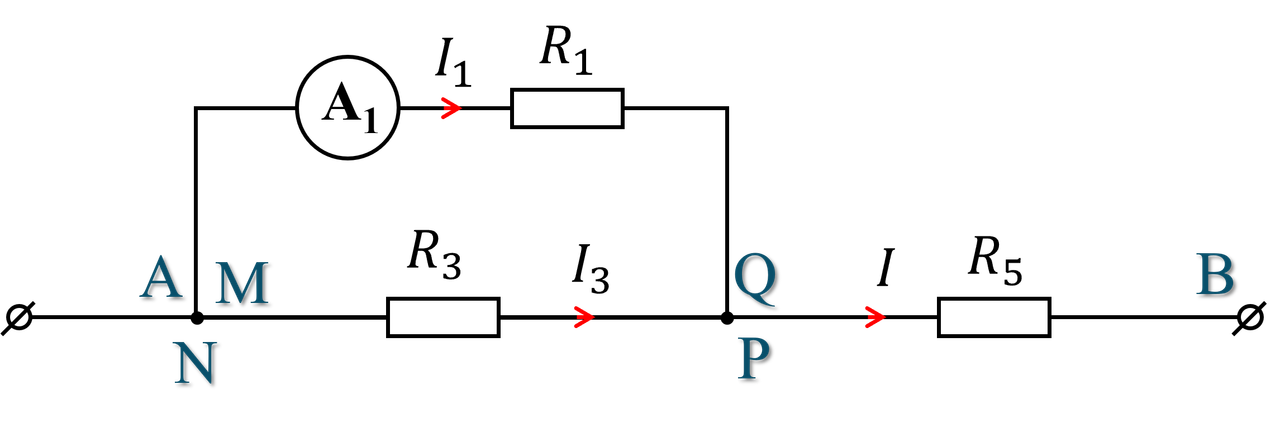
$$R_{13}=\frac{R}{2}\\ R_\text{tđ}=R_{13}+R=\frac{3}{2}R\\ I=\frac{U}{R_\text{tđ}}=\frac{2U}{3R}$$ Do $R_1=R_3=R$ nên $$I_1=I_3=\frac{I}{2}=\frac{U}{3R}$$

Để có đầy đủ các dòng điện, ta biểu diễn các dòng điện trong mạch đầy đủ. Và chú ý rằng chỉ có dòng điện chạy trong các nhánh của mạch mới (Hình 2), các nhánh không có trong Hình 2 thì không có dòng điện chạy qua. Ta vẽ lại mạch tổng thể như hình dưới đây:

Hình 4: Dòng điện không chạy qua $R_2$ và các vôn kế.

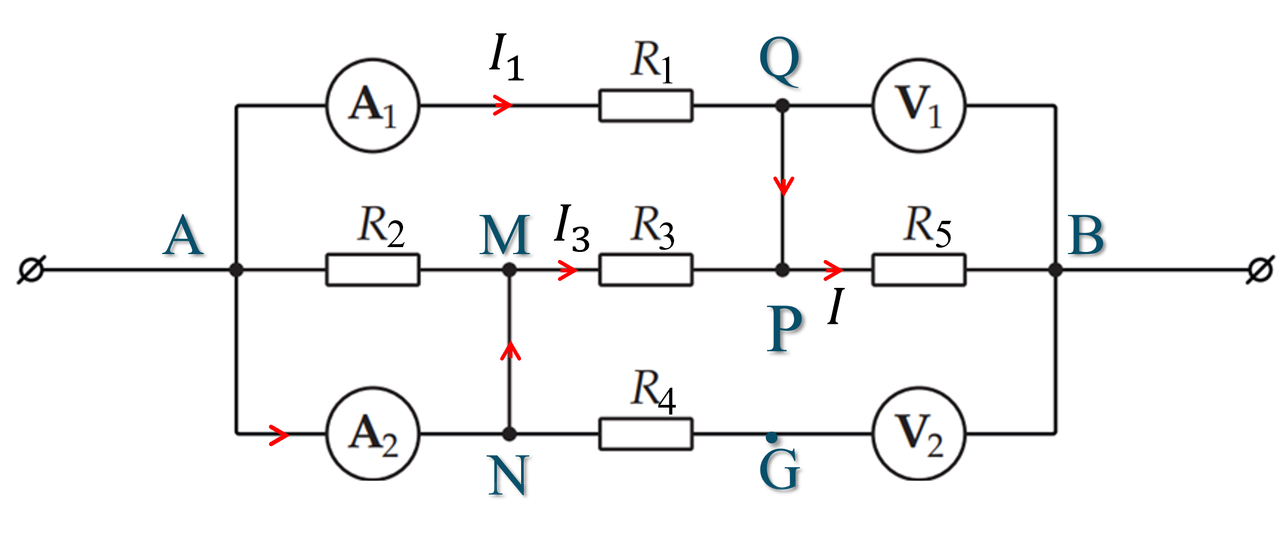
Từ Hình 4 ta thấy số chỉ ampe kế $\text{A}_2$ chính là $I_3$, tức là $$I_3=20\ \text{mA}$$ Và theo đó thì số chỉ ampe kế $\text{A}_1$ là $I_1$ cũng bằng $I_3$ và bằng $$I_1=20\ \text{mA}$$ Số chỉ vôn kế $\text{V}_2$ là $U_\text{GB}=U_\text{NB}$, bởi vì dòng điện qua $R_4$ bằng không nên $U_\text{NG}=0$. Mà theo Hình 3 thì $U_\text{NB}=U$. Như vậy $$U=6\ \text{V}$$ Số chỉ vôn kế $\text{V}_1$ là $$\begin{align} U_{\text{V}_1}=U_\text{QB}&=IR_5\\ &=\frac{2U}{3R}R\\ &=\frac{2U}{3}=4\ \text{V} \end{align}$$ 2. Tính điện trở $R$
$$\begin{align} R=R_5&=\frac{U_{\text{V}_1}}{I}\\ &=\frac{4}{2\cdot 20}\\ &=0.1\ \text{k}\Omega \end{align}$$ 3. Đổi chỗ ampe kế $\text{A}_2$ với vôn kế $\text{V}_2$
Bỏ các vôn kế đi, ta vẽ lại mạch như Hình 5 như sau:

Hình 5: Mạch điện là mạch cầu cân bằng.

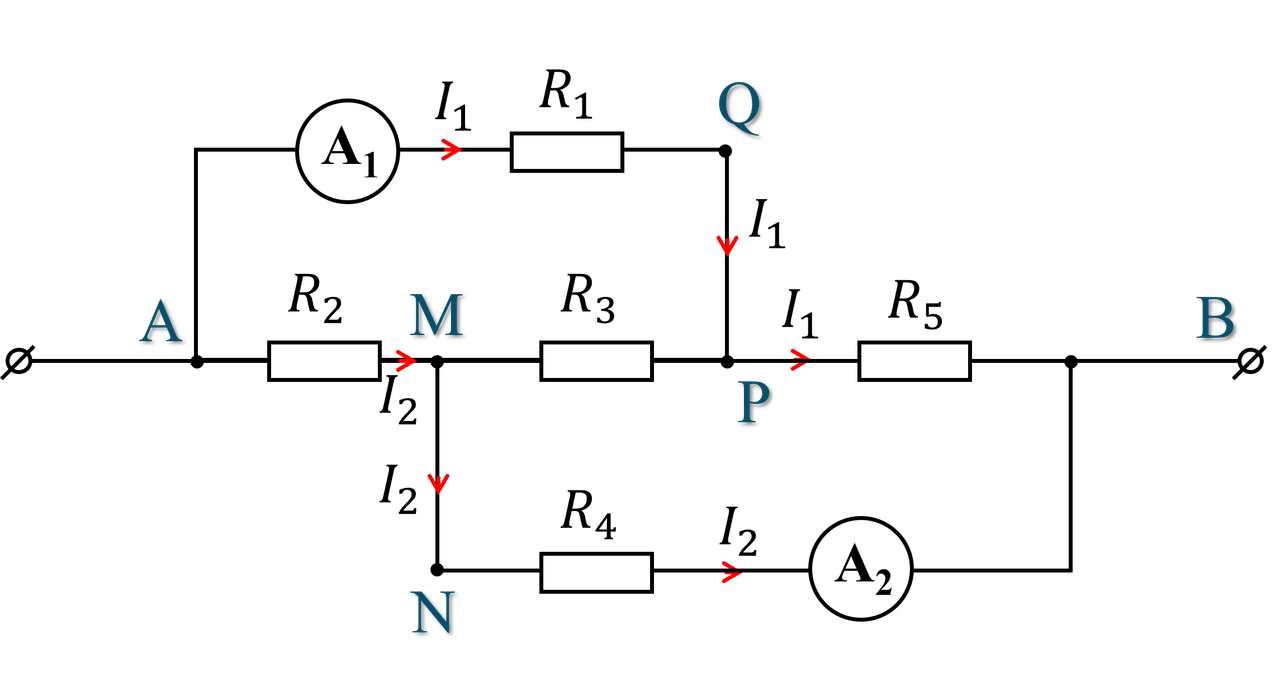
Vì các điện trở giống nhau nên đây là mạch cầu cân bằng, và do đó không có dòng điện chạy qua cầu $R_3$, cường độ dòng điện qua các nhánh là bằng nhau $$\begin{align} I_1=I_2&=\frac{U}{2R}\\ &=\frac{6}{2\cdot 0.1}\\ &=30\ \text{mA} \end{align}$$ Số chỉ các ampe kế bằng nhau và bằng 30 mA.
Số chỉ các vôn kế cũng bằng nhau: $$U_{\text{V}_1}=U_{\text{V}_2}=\frac{U}{2}=3\ \text{V}$$

Câu IV

1. Khoảng cách ảnh - vật

Hình 6: Sự tạo ảnh của một điểm sáng nhưng ta vẽ dạng đoạn thẳng để đơn giản hơn và dễ tính toán hơn.

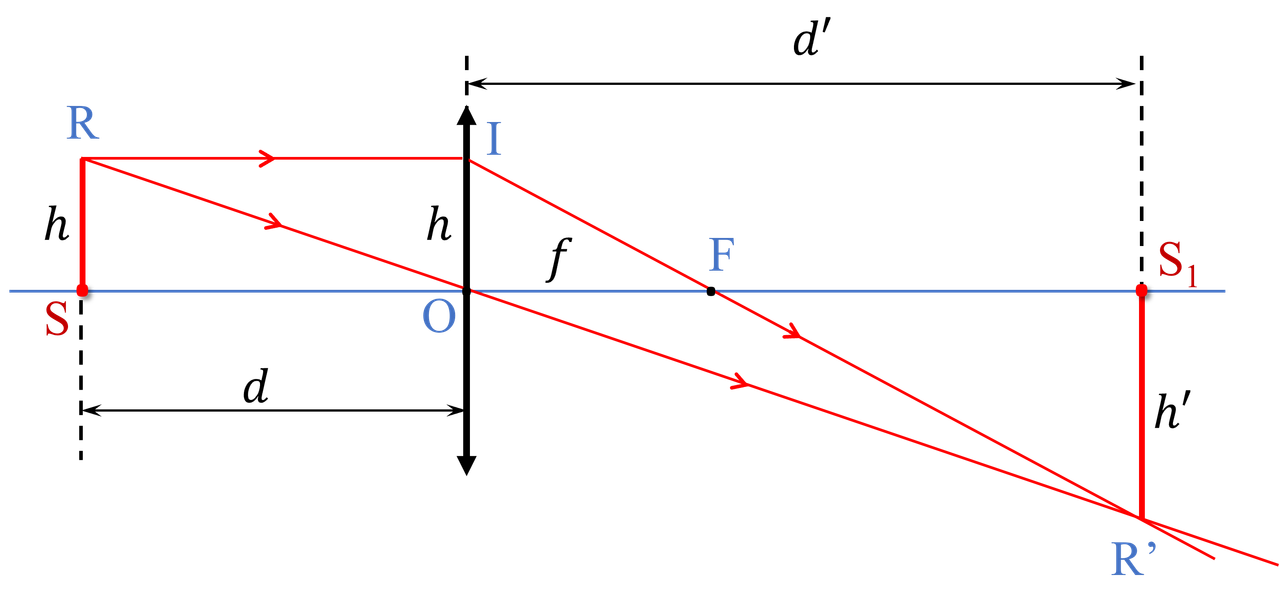
Từ hình vẽ ta có: $$\frac{h'}{h}=\frac{d'}{d}=\frac{d'-f}{f}=\frac{f}{d-f}\\ $$ $$\begin{align} d'&=\frac{df}{d-f}\\ &=\frac{15\cdot 10}{15-10}\\ &=30\ \text{cm} \end{align}$$

Khoảng cách giữa ảnh và vật là $$SS_1=d+d'=15+30=45\ \text{cm}$$ 2. Đổi thấu kính hội tụ bằng thấu kính phân kì
Ta vẽ hình như Hình 7 sau đây.

Hình 7: Sự tạo ảnh của thấu kính phân kì.

$$\frac{h''}{h}=\frac{d''}{d}=\frac{f-d''}{f}$$ $$\begin{align} d''&=\frac{df}{d+f}\\ &=\frac{15\cdot 10}{15+10}\\ &=6\ \text{cm} \end{align}$$ Khoảng cách giữa hai ảnh $$S_1S_2=d''+d'=6+30=36\ \text{cm}$$ 3. Đặt $\text{L}_2$ sao cho tia tới và tia ló cùng song song với trục chính
Tia tới $\text{L}_1$ (ta đặt là tia (1)) song song với trục chính thì tia ló ra khỏi $\text{L}_1$ sẽ đi qua tiêu điểm $\text{F}_1$ của thấu kính này (ta đặt tia này là tia (2)). Tia (2) tới thấu kính $\text{L}_2$, tia ló ra khỏi $\text{L}_2$ là tia (3). Để tia (3) cũng song song với trục chính thì tia (2) phải đi qua tiêu điểm $\text{F}_2$ cả thấu kính $\text{L}_2$, như Hình 8 dưới đây.

Hình 8: Tia sáng tới song song với trục chính cho tia ló cũng song song với trục chính.

Vậy tia (2) đi qua cả $\text{F}_1$ và $\text{F}_2$, tức là tiêu điểm của hai thấu kính trùng nhau. Trong khi tiêu cự hai thấu kính bằng nhau, suuy ra phải đặt hai thấu kính sát nhau. Khoảng cách giwxh hai thấu kính $\ell=0$.

Câu V

Đo điện trở một cách chính xác nhất.
Để tăng độ chính xác của phép đo, bạn có thể làm như sau: Đầu tiên, dựng mạch điện theo sơ đồ như hình 9.

Hình 9: Mắc mạch điện để đo điện trở ampe kế.

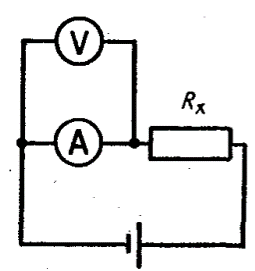
Ta xác định được điện trở của ampe kế $r_\text{A}$: $$r_\text{A}=\frac{U_1}{I_1}$$ trong đó $I_1$ và $U_1$ là số chỉ của ampe kế và vôn kế.
Sau đó lắp mạch điện theo sơ đồ như Hình 10.

Hình 10: Mắc mạch điện để đo điện trở $R_x$.

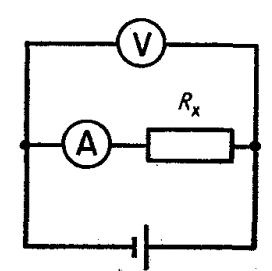
Và từ phương trình $$I_2\left(R_x+r_\text{A}\right)=U_2$$ Trong đó $I_2$ và $U_2$ là số chỉ của ampe kế và vôn kế. Suy ra điện trở $R_x$: $$R_x=\frac{U_2}{I_2}-r_\text{A}=\frac{U_2}{I_2}-\frac{U_1}{I_1}$$

---

---