Câu 1. Cơ - 2,5 điểm
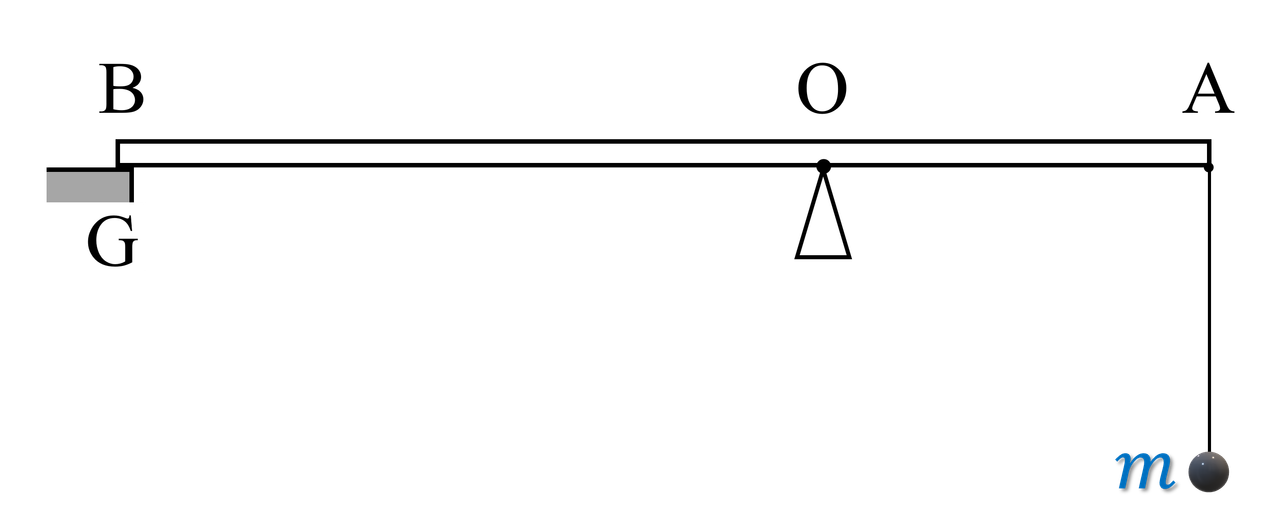
Một tấm ván AB mỏng, đồng chất, có độ dài $l = 1\text{,}6\ \text{m}$, khối lượng $m_1 = 4\text{,}5\ \text{kg}$ có thể quay quanh một trục cố định O $\left(OA = 40\ \text{cm}\right)$ và được tựa lên một giá đỡ $\text{G}$ để ván có vị trí nằm ngang. Lấy $g = 10\ \text{m/s}^2$.
Đặt một vật khối lượng $m_2 = 6\ \text{kg}$ vào đầu $\text{B}$, hệ số ma sát trượt giữa vật và ván là $\mu$. Hỏi phải truyền cho vật tốc độ nhỏ nhất bằng bao nhiêu dọc theo ván để ván có thể quay quanh $\text{O}$?
Nếu treo vật khối lượng $m = 2\ \text{kg}$ vào đầu $\text{A}$ bởi một sợi dây thì thấy ván không quay. Làm cho dây lệch khỏi phương thẳng đứng một góc $90^0$ (hình 1) rồi buông nhẹ, ván bắt đầu quay quanh $\text{O}$ khi dây hợp với phương thẳng đứng một góc $\alpha$. Tính góc $\alpha$.
Lời giải
1) Vận tốc ban đầu nhỏ nhất
Giả sử khi $m_2$ ở D cách O một đoạn $x$ thì ván quay quanh O, khi đó $$m_1g\frac{l}{4}=m_2gx\\ \Rightarrow x=\frac{m_1}{m_2}\frac{l}{4}=0.3\ \text{cm}$$ + Quãng đường mà $m_2$ đi từ B đến vị trí ván quay là: $$s=1.2+0.3=1.5\ \text{cm}$$ + Áp dụng định lí động năng $$\frac{1}{2}m_2v_0^2=\mu m_2gs\\ \Rightarrow v_0=\sqrt{2\mu gs}=3\ \text{m/s}$$
2) Góc giữa sợi dây và phương thẳng đứng
Để ván quay quanh O thì lực đặt vào A có thành phần thẳng đứng thỏa mãn:
$$m_1g\cdot OC\le F\cdot OA$$
Do $OC=OA$ suy ra $m_1g \le F$.
+ Xét vật $m$:
$$T-mg\cos{\alpha}=m\frac{v^2}{l}\\
mgh=\frac{mv^2}{2}, h=l\cos{\alpha}\\
\Rightarrow \frac{v^2}{l}=2g\cos{\alpha}
$$
Kết hợp các phương trình ta suy ra
$$
T=3mg\cos{\alpha}
$$
Mặt khác
$$F=T\cos{\alpha}=3mg\cos^2{\alpha}$$
Để ván quay thì
$$F_\text{min}=m_1g$$
Vậy
$$3mg\cos^2{\alpha}=m_1g\\
\Rightarrow \cos^{\alpha}=\frac{m_1}{3m}=\frac{4.5}{6}\\
\alpha=30^0
$$

0 nhận xét:
Đăng nhận xét